I) Coordonnés d’un point dans un repère :
VID1
Application 01:
- représenter les points suivant dans un repère orthonormé . U(2;3),K(-2;4),L(-1;-2),M(3;-5),N(3;0),P(-4;0),W(0;5)\:et\:S(0;-3)
- Donner les cordonnés des points représentés dans cette repère :
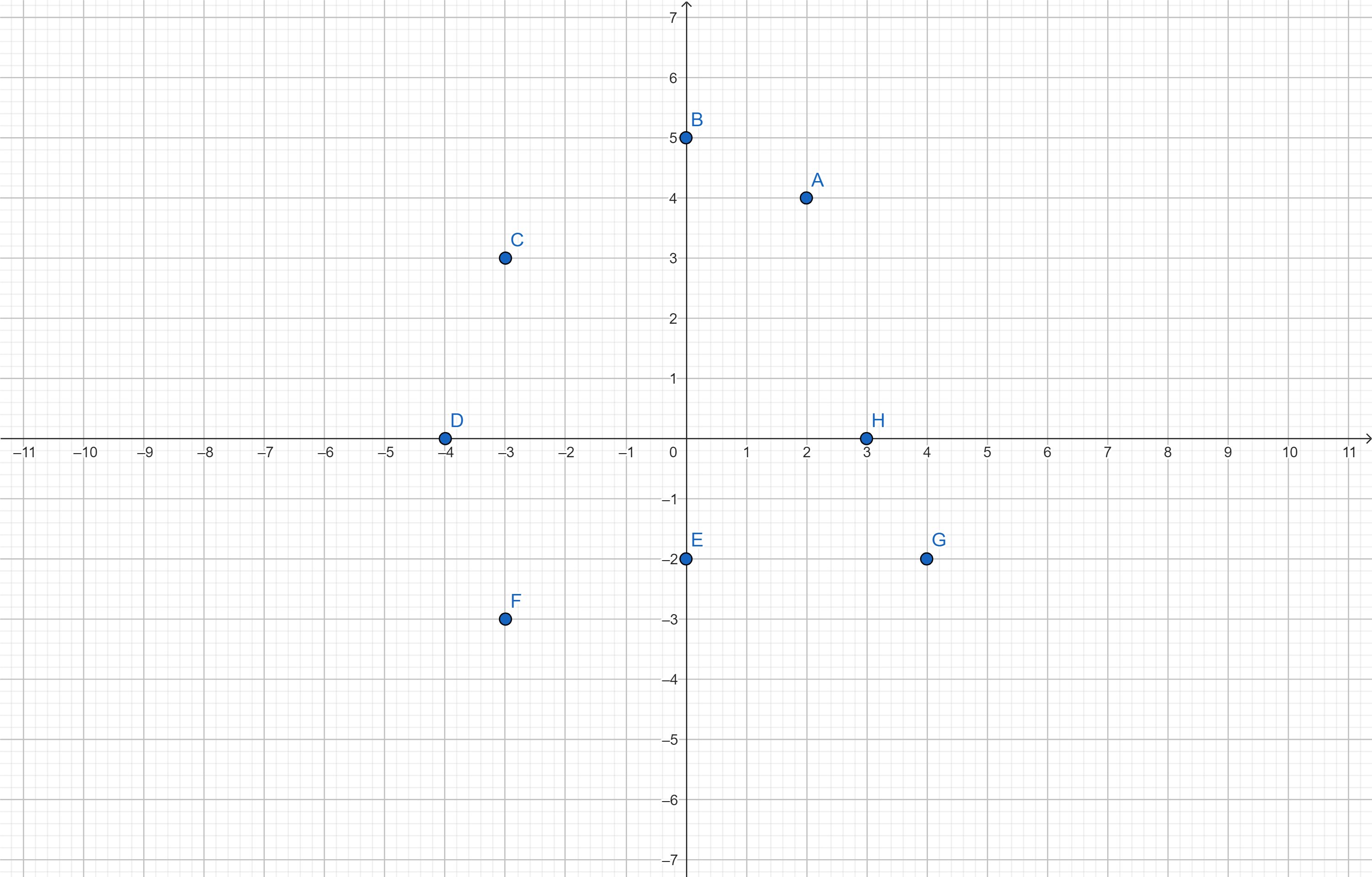
I) Coordonnés d’un vecteur,somme vecteurs et vecteurs egaux dans un repère :
1/ coordonnés d’un vecteur:
Règle 01 ⇲ coordonnées d’un vecteur
\boxed{si \:A(x_{A};y_{A})\:et \:B(x_{B};y_{B})\\Alors \:\overrightarrow{AB} (x_{B}-x_{A};y_{B}-y_{A}) }vid2
Application 02:
soient : A(2;3),B(-2;4),C(-1;-2),D(3;-5),E(3;0),F(-4;0),G(0;5)\:et\:H(0;-3)
- Donner les coordonnés des vecteurs : \overrightarrow{AB}, \overrightarrow{Ac}, \overrightarrow{BD}, \overrightarrow{EF}, \overrightarrow{AE}, \overrightarrow{BG}\:et\:\overrightarrow{CH}
1/ coordonnés somme vecteurs et vecteurs égaux:
Règle 02 ⇲ coordonnées somme de deux vecteurs
\boxed{si \:\overrightarrow{AB}(a;b)\:et\;\overrightarrow{EF}(c;d)\;Alors \:(\overrightarrow{AB}\:+\overrightarrow{EF})(a+c;b+d) }Règle 03 ⇲ égalité de deux vecteurs
\boxed{\:\overrightarrow{AB}=\;\overrightarrow{EF}=\;signifie \;que\;: \: \begin{cases}x_{B}-x_{A}=x_{F}-x_{E} \\y_{B}-y_{A}=y_{F}-y_{E}\end{cases}}vid3
Application 03:
soient A(5;-3),B(-2;1),E(5;-4),M(-6;-4)\:et\:C(-6;-3)
- déterminer les coordonnées du point D tes que ABCD soit un parallélogramme
- déterminer les coordonnées du point F tes que : \overrightarrow{AF} = \overrightarrow{AB}+\overrightarrow{AM}
- Monter que le quadrilatère AEMC est un parallélogramme. ( indication : montrer que \overrightarrow{AE}=\overrightarrow{CM} )
I) Coordonnés de milieux d’un segment dans un repère :
Règle 04 ⇲ coordonnées de milieu d’un segment
\boxed{\: I \;le \;milieu\; de\; [AB]\;signifie \;que\;: \: I(\frac{x_{B}+x_{A}}{2};\frac{y_{B}+y_{A}}{2})}vid4
Application 04:
soient A(1;-4),B(3;-5),C(2;5)\:et\:D(0;6)
- déterminer les coordonnées du milieu de segment [AC]
- déterminer les coordonnées du milieu de segment [BD]
- Que peut-on déduire. (pour le quadrilatère ABCD )




