I) Définition d’un système :
Application 01:
on considère le système : (S) : \begin{cases} 5x-2y &=-1 \\ 3x-y &=0 \end{cases}
- Montrer que le couple (1;3) est une solution de (S).
- Est ce que le couple (1;4) est une solution de (S).
II) Résolution d’un système :
1/ la méthode de substitution :
Application 02:
résoudre les systèmes suivants par la méthode de substitution :
(S_{1}) : \begin{cases} 3x+y &=5 \\ 2x+3y &=8 \end{cases} \:\: (S_{2}) : \begin{cases} 3x+2y &=-4 \\ 2x+y &=-3 \end{cases} \:\: (S_{3}) : \begin{cases} x+4y &=14 \\ 5x+2y &=16 \end{cases}
Indication des réponses ‘application 02’
La solution de (S_{1}): \:le\:couple\: (1;2)
La solution de (S_{2}): \:le\:couple\: (-2;1)
La solution de (S_{3}): \:le\:couple\: (2;3)
2/ la méthode de la combinaison linéaire:
Application 03:
résoudre les systèmes suivants par la méthode de la combinaison linéaire :
(S_{4}) : \begin{cases} 3x+2y &=-1 \\ 5x+y &=-4 \end{cases} \:\: (S_{5}) : \begin{cases} 4x-y &=9\\ -2x+3y &=-7 \end{cases} \:\: (S_{6}) : \begin{cases} -5x+2y &=-19\\ 10x+3y &=24 \end{cases}
Indication des réponses ‘application 03’
La solution de (S_{1}): \:le\:couple\: (-1;1)
La solution de (S_{2}): \:le\:couple\: (2;-1)
La solution de (S_{3}): \:le\:couple\: (3;-2)
2/ la méthode graphique:
Application 04:
- résoudre graphiquement le système (S_{7}) : \begin{cases} 2x+y &=4 \\ x+3y &=7 \end{cases}
- résoudre graphiquement le système (S_{8}) : \begin{cases} 5x-2y &=12 \\ 3x+y &=5 \end{cases}
- résoudre graphiquement le système (S_{9}) : \begin{cases} 3x+2y &=7 \\ x+3y &=7 \end{cases}
- résoudre graphiquement le système (S_{10}) : \begin{cases} 5x-2y &=7 \\ 3x+y &=2 \end{cases}
Indication des réponses ‘application 03’
La solution de (S_{7}): \:le\:couple\: (1;2)
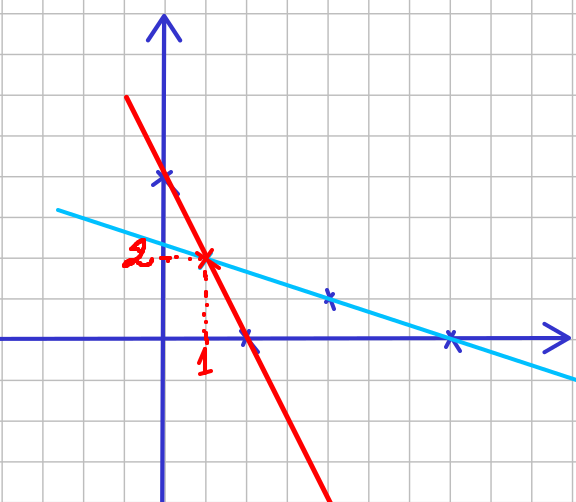
La solution de (S_{8}): \:le\:couple\: (2;-1)
La solution de (S_{9}): \:le\:couple\: (;)
La solution de (S_{10}): \:le\:couple\: (;)



